楕円曲線と有理点

$\mathbb{Q}$上定義された楕円曲線とは、$a_1$, $a_2, \cdots, a_6 \in \mathbb{Q}$に対し、 $$ y^2 + a_1 xy + a_3 y = x^3 + a_2 x^2 + a_4 x + a_6 $$ で表される曲線です。ただし2次曲線の場合と同様、退化する場合は除いておきます。 この曲線は $$ y^2 = x^3 + ax +b, \qquad (a,b \in \mathbb{Q}) $$ という形の標準形へ持って行くことができることが知られています。このとき、 退化するのは「右辺=0」という方程式が重根を持つ場合、 つまり判別式 $\Delta := -16(4a^2-27b^2)$が$0$となるときです。上の方程式で表される楕円曲線を$E$と書き、 その有理点全体の集合を $E(\mathbb{Q})$と記します。ただし無限遠点を１つ余分に付け加えておきます。 すなわち、 $$ E(\mathbb{Q}) := \{ (x,y) \in \mathbb{Q}^2 \mid y^2= x^3 + ax + b \} \cup \{ \infty \} $$ とします。 それでは、様々な楕円曲線に対して、有理点はどれだけあるのでしょうか？ 何個か知られている例をあげてみます。

  

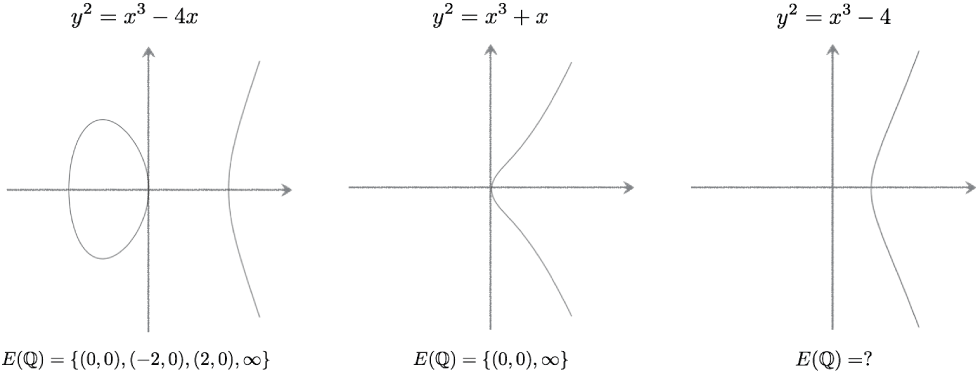
点の数が有限個の場合もありますし、点の数が無限個の場合もあることが知られています。 ２次曲線の場合と様子が違うことが見て取れます。楕円曲線では有理点の個数が大きく 変動することが知られています。これは、楕円曲線が２次曲線の様な パラメーター表示を持たないことかが知られていることにも起因しています。

楕円曲線の有理点の演算

例えば楕円曲線に$1$つ有理点があったとして、その点を通る直線を考えると、その直線は 楕円曲線と合計$3$点で交わり、最初の点が有理点で直線の傾きが有理点だとしても、 残りの$2$点が有理点であるとは限りません。楕円曲線の場合、パラメーター表示に代わる 何かはあるのでしょうか？

楕円曲線の$2$つの点 $P$, $Q$に対して、その２点を通る直線は、楕円曲線と３点目 $R’$ で交わります。 $P$, $Q$が有理点であるとすると、そこを通る直線の傾きも有理数となり、点 $R’$も有理点になることが 分かります。また、楕円曲線の式からグラフは$x$軸に対して対称となることから、点$R’$を$x$軸で ひっくり返した点$R$も有理点となることが分かります。以後、この様に得られた点 $R$ を、 $R = P+ Q$と書きます。ここで$+$という記号を使っていますが、普通の有理数の足し算という意味ではありません。 ２つの有理点$P$, $Q$に対して、新しい有理点$R$を対応させる操作という意味です。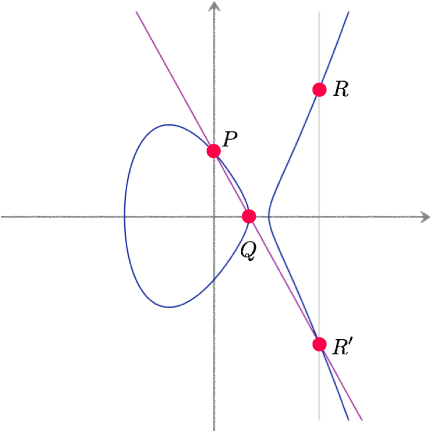

楕円曲線の有理点$P$が与えられたとき、$P+P$は$P$での接線を使って定義します。この点を$2P$と書きます。この操作で$3P = 2P + P$、$4P = 3P +P$と順番に有理点が定まって行きます。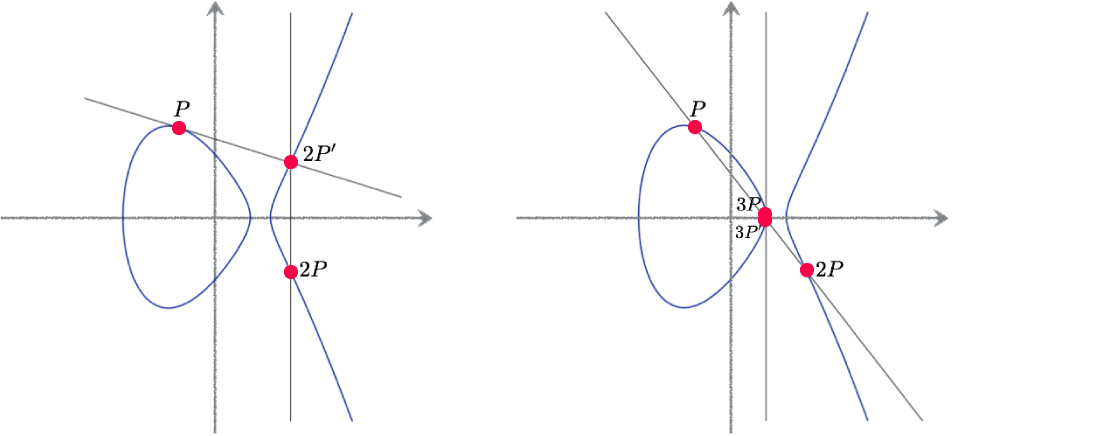

また、２点$P,Q$を結ぶ直線の傾きが$\infty$になるとき、$P+Q = \infty$と定義します。同様に、点$P$での接線の傾きが$\infty$となるときも $2P = \infty$と定義します。最初にあげた楕円曲線の例で、$y^2=x^3-4x$ や $y^2=x^3+x$の有理点に上の操作を施すと、すぐに$\infty$となってしまいますが、 $y^2=x^3-4$の有理点$P=(2,2)$を考えると、実は、$2P, 3P, \cdots$は全て異なる有理点となることが知られています。従ってこの場合、 $E(\mathbb{Q})$は無限集合になることが導かれます。

Mordellの定理とBirchとSwinnerton-Dyer予想

以上の考察から、楕円曲線の有理点は二次曲線の場合とは異なり、有理点の数が有限個だったり無限個だったりと複雑な振る舞いをしていることが分かります。 これに関して、以下の大事な結果が知られています。

Mordellの定理　$E(\mathbb{Q})$は、有限個の有理点 $P_1, \cdots, P_n$から上記の操作で生成される。

Mordellの定理が主張していることは、$E(\mathbb{Q})$のどの点も、$P_1, \cdots, P_n$という有限個の有理点の和として求まるということです。$E(\mathbb{Q})$自身は無限集合かもしれませんが、無限集合であったとしても有限個の有理点から操作を始めると全ての有理点が求まってしまうというところが、とても不思議で面白いところです。

楕円曲線が与えられたとき、その楕円曲線の有理点を見つけるための有効なアルゴリズムは現在のところ知られていません。有理点が与えられれば、上の操作を使って新しい有理点を作ることもできますが、楕円曲線の有理点すべてを具体的に求めることは非常に興味深い問題でありながら、現在人類の持つ技術では難しい問題でもあります。この様な状況の中、与えられた楕円曲線の有理点の個数の大きさを予想しているのがBirch and Swinnerton-Dyer予想です。

Birch and Swinnerton-Dyer予想（BSD予想）は、楕円曲線の有理点の大きさが、$L$関数と呼ばれる関数で記述されると予想しています。 この予想は、幾何学的な対象の数論的な情報と$L$関数の関係を調べるという、整数論と呼ばれる数学分野の中心的なテーマの１つであり、今後取り組むべき重要な７つの問題としてクレイ数学研究所により選ばれたミレニアム懸賞問題の１つでもある、とても大切な問題です。 多くの数値実験などにより、この予想が正しいことが期待されていますが、現在のところはまだ限られた楕円曲線に対してしか証明されていません。 BSD予想は、Deligne予想、Beilinson予想、Bloch-Katoの玉河数予想など、方程式で定義された幾何学的図形の数論的な情報と $L$関数との関係を記述する様々な予想の出発点となっています。

• 「楕円曲線の数論幾何」伊藤哲史先生（京都大学）のスライド

 

 

※2016年2月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。