「これまで誰もみたことない新しいものをみてみたい」純粋で熱い気持ちがあれば、自分も数学の進展に貢献できるかもしれない。そんな勇気と希望をお届けするこのコラムでは、マージョリー・ライス(Marjorie Rice)さんという女性のアマチュア研究者の話を取り上げます。

　ライスさんが取り組んだのは、敷き詰めという数学の問題です。平面にぴったり敷き詰められるタイルはどんな形？という子供にもとっつき易く、実は奥の深い問題です。タイル同士が重なりなく隙間なくどこまでも敷き詰められる条件等を見つけることが主な課題です。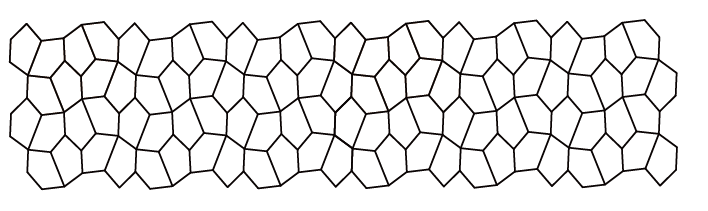

ライスさんの取り組んだ敷き詰めの問題
合同の凸五角形タイルで平面を敷き詰めることができる

　ライスさんがこの問題を知るきっかけとなったのは、科学雑誌に掲載された二回にわたるコラムでした。当時ライスさんは5人の子供を持つ50代前半の主婦で、科学雑誌は子供向けに購読していたようです。ライスさんは高校時代に数学に興味があったようですが、卒業後は数学とは縁遠い生活だったそうです。

　ライスさんが読んだ初めのコラムには、一種類のタイルだけで平面を敷き詰められるタイルの最新研究の成果が紹介されていました。一種類のタイルが三角形や四角形の場合はどのような形状でも敷き詰められるのですが、タイルが五角形の場合は特殊な形状に限られるというのです。特にどの頂点でも角張った凸形状に限定すると８種類の凸五角形タイルが得られたことがコラムでは紹介されていました。

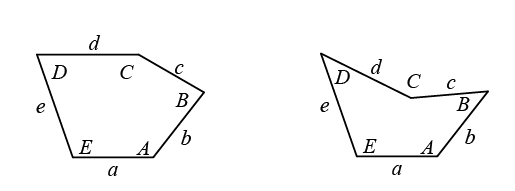
どの頂点でも角張った凸五角形(左)と、角ばっていない頂点Cを含む凹五角形(右)の例

　「平面を敷き詰められる新種の凸五角形タイルを、自分でも見つけられるかもしれない」とライスさんを含め多くのコラムの読者は思ったことでしょう。子供にもとっつき易いタイルの話なので、タイルを作りうまく並べ変えれば答えにたどり着けると簡単に思うかもしれません。

　二回目のコラムでライスさんはコンピュータ研究者が新種の凸五角形タイルを発見したことを知ります。その新種の凸五角形タイルは、明らかにそれまでの８種類とは角度と辺の条件が異なるものでした。その敷き詰めを確認しても裏返しも含めて確かに一種類の凸五角形タイルからできていました。

　この新種の発見を聞いてライスさんはどのように感じたでしょう。このコンピュータ研究者が実際にコンピュータを利用したか定かではないですが、もしコンピュータが新種を発見したと聞いたら、もう太刀打ちできないとこの新種の発見に興味を失う人もいたかもしれません。この時代コンピュータを用いて数学の難問であった四色問題が解かれるなど、コンピュータが数学にも影響を見せはじめた時期でもありました。

　ライスさんは新種発見へのこだわりよりも、凸五角形タイルの本質を理解したいと思ったようです。ライスさんは９種類の凸五角形タイルをつぶさに観察し、それらの違いを自分の言葉で書き下していきました。 そして凸五角形タイルにのめり込むこと数ヶ月後ライスさんは新種の凸五角形タイルを発見します。ライスさんはコラムの作者に手紙を送り、専門の数学者による検証が行われました。検証結果によりライスさんの発見が従来の研究の抜け漏れを埋める正しいものであることが明らかになったのです。

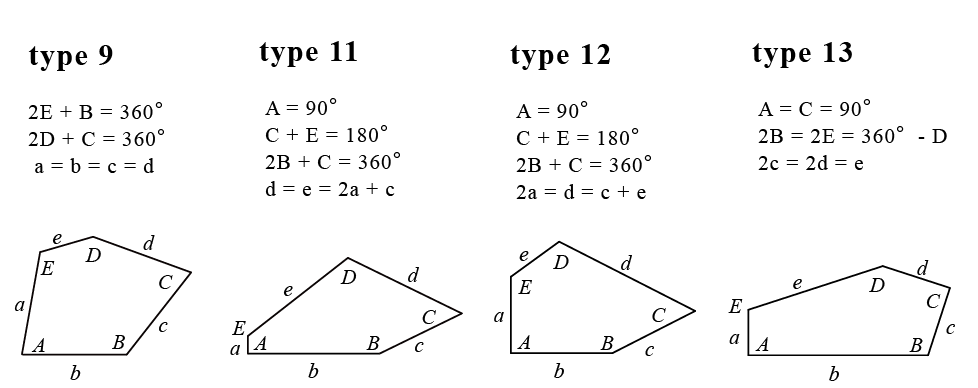
ライスさんが発見した平面を敷き詰める凸五角形の４種類の条件とその例

　その後ライスさんは検証を担当した数学者との交流を深め、さらに３種類の凸五角形タイルを発見します。振り返ってみると、現在までに判明している凸五角形タイルの４分の１以上の種類をライスさんが発見したことになります。

　ライスさんを魅了した敷き詰められる凸五角形の問題は、実は2016年暮れの現在もなお未解決のままです。最近では2015年の夏にコンピュータを利用して新種の凸五角形タイルが発見されていますが、これ以上新種がないことの証明はできていません。

　もしかしたら現在90歳過ぎのライスさんもまだこの未解決問題に取り組んでいるかもしれません。平面を敷き詰める凸五角形の問題に終止符を打つのは、ライスさんでしょうか、コンピュータでしょうか、それともこのコラムの読者のあなたでしょうか。

　ライスさんはこの問題に取り組む過程で、敷き詰めの多様な世界に出会いました。
次回は、ライスさんの敷き詰めへのさらなる探究をご紹介したいと思います。

参考リンク

ライスさんのホームページ
ライスさんによる解説記事 
ライスさんの結果を検証を担当した数学者による解説記事

※2016年12月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。