私は中学生の頃からベースやギターを弾くことが趣味で、現在もバンドを組んでいるほど音楽が大好きな学生です。また同時に数学も大好きで、いつからか「数学と音楽の間にはどのような関係があるのだろう？」と思うようになりました。そんなとき、数学と音楽に関する次の話題が「数学活用」という教科書に載っているのを見つけました。

五線譜上に音符を3つ積み重ねてできる和音は、ドミソ、ミソシ、など全部で7種類あります。

それぞれの和音に対し、和音を作る3つの音を角に持つ三角形を作り、共通する2つの音を持つ辺を張り合わせていくと、なんと「メビウスの帯」と呼ばれる数学的な図形ができあがるのです。

 

 

 

 

 

 

 

 

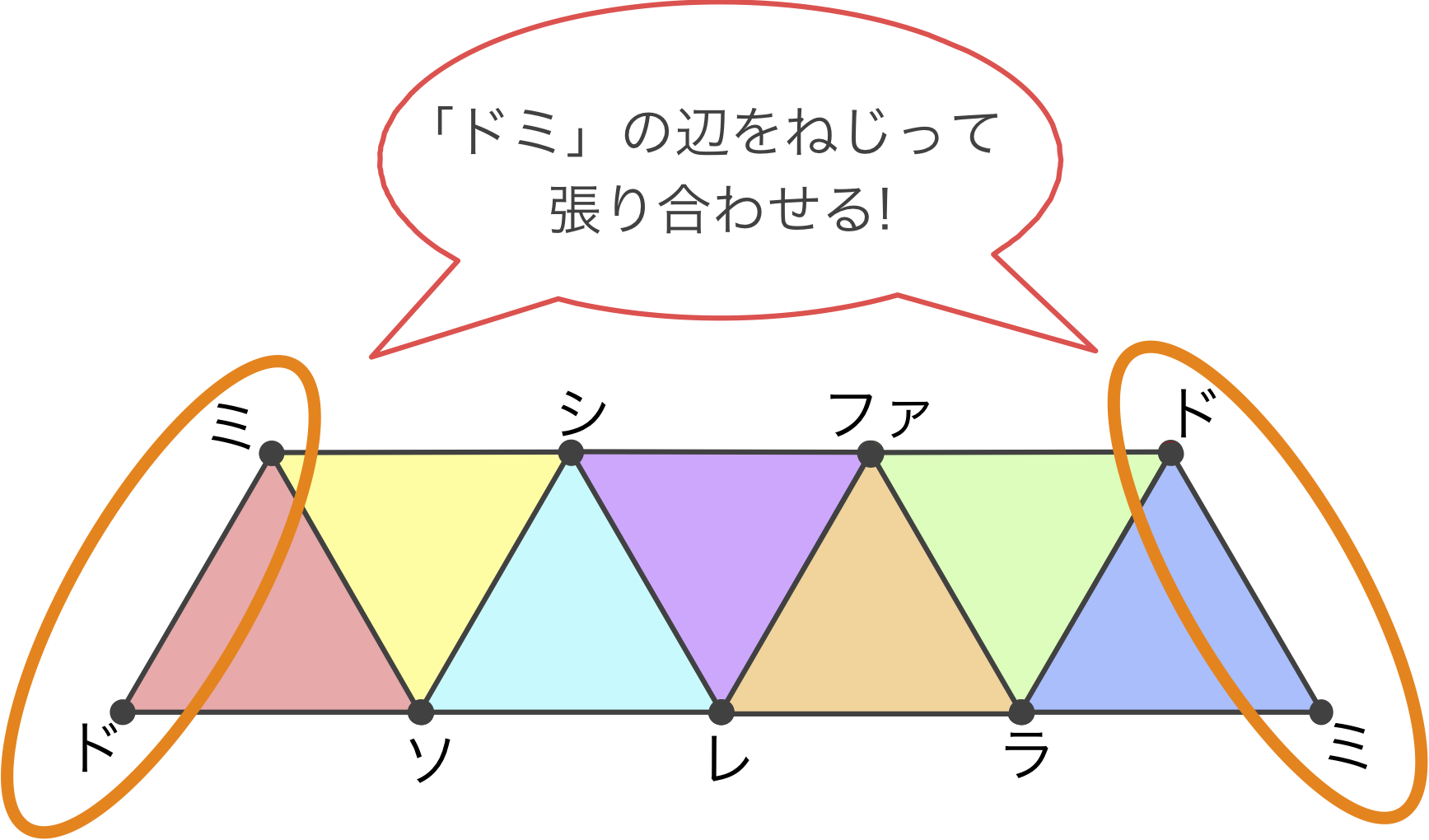
　　　　　　　私はこのお話を読み、幾何的な視点から数学と音楽の関係性について述べていることにとても感動しました。そして、これだけでも十分面白い内容ですが、先ほどの7つの和音の三角形を使って、メビウスの帯以外にどんな図形を作ることができるのか疑問に思い、実際に研究をしてみることにしました。今回は具体的に「正八面体」と「正二十面体」という2種類の正多面体を例に見ていきましょう。

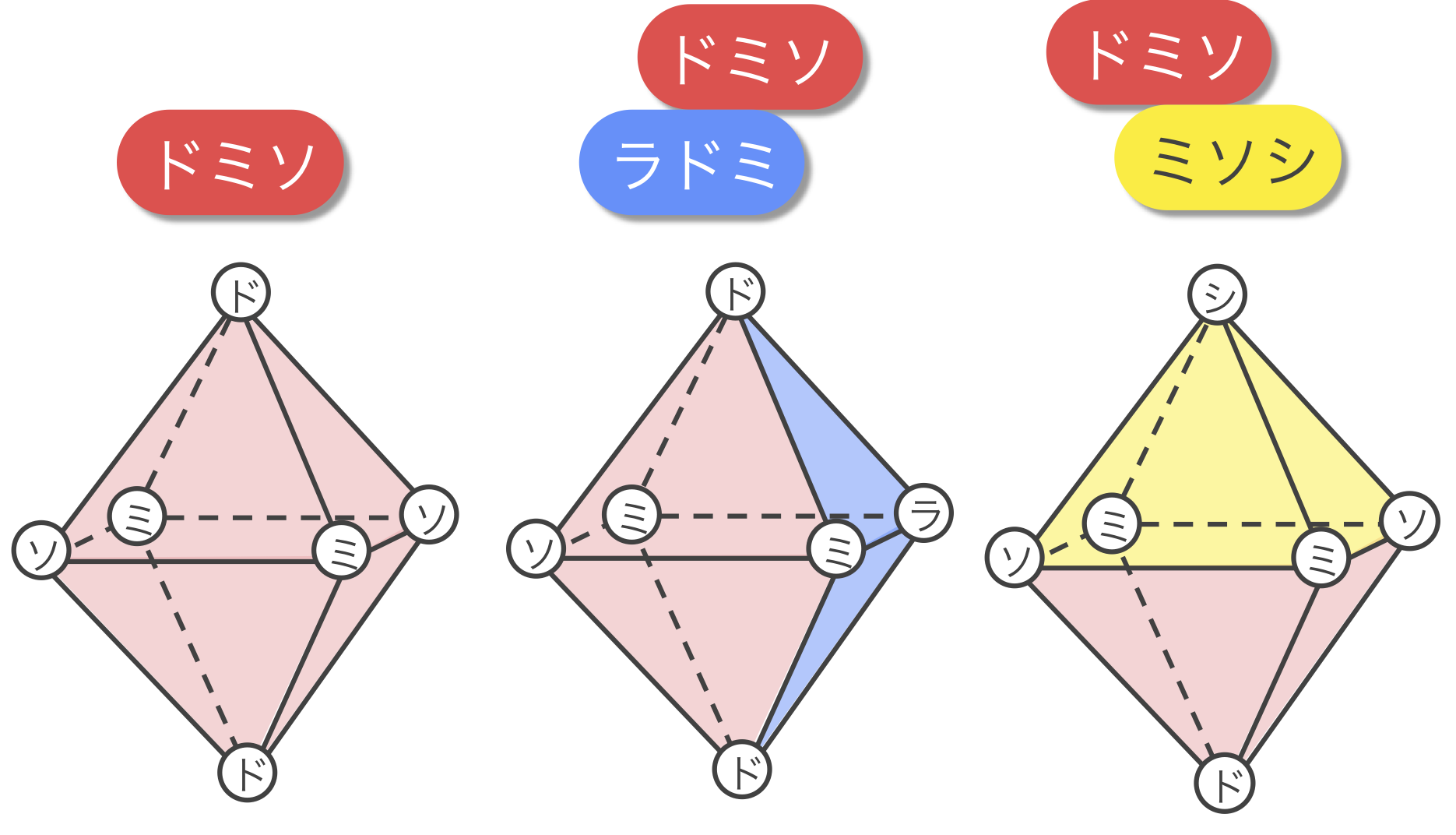
まず、正八面体は下図のように、1種類もしくは2種類の和音の三角形を使って作ることができます。しかし、2種類の和音の三角形から作られる正八面体にもう1種類別の和音の三角形を加えようとすると矛盾が生じ、正八面体を作ることができなくなってしまいます。よって、正八面体は1種類または2種類の和音の三角形から作ることができるということがわかりました。(ぜひ実際に手を動かして作ってみて下さい。)

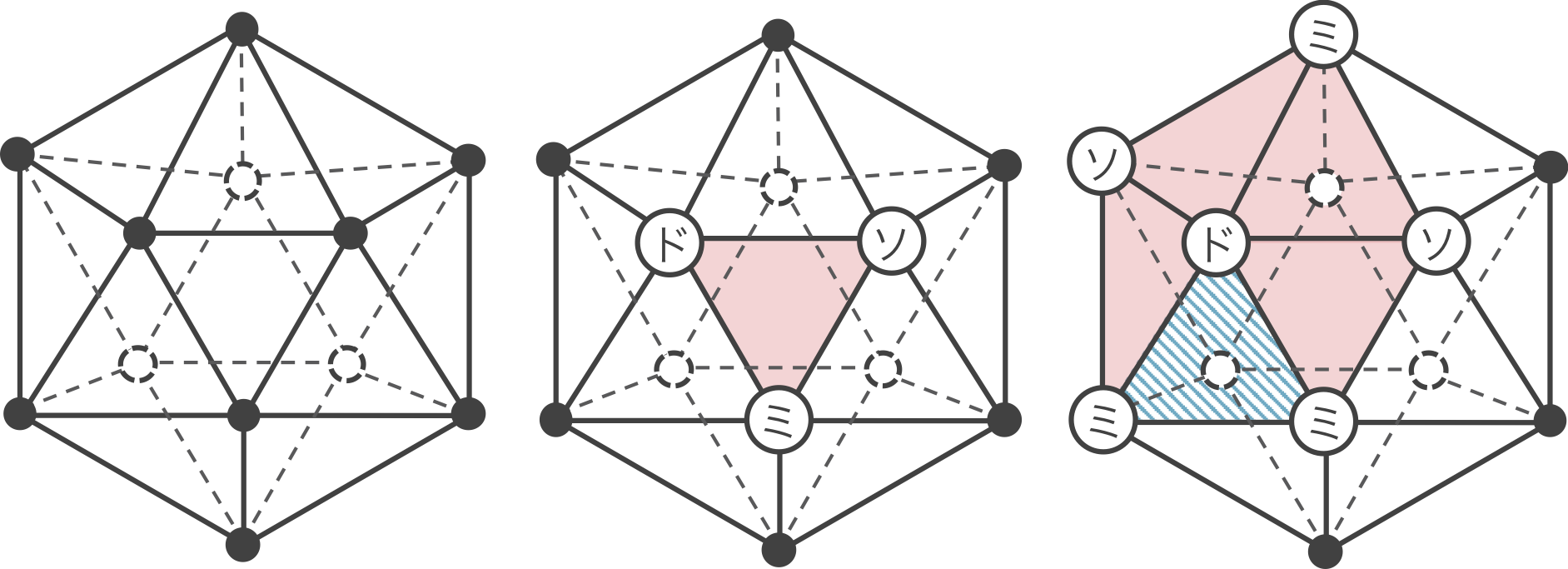
では、正二十面体についても調べてみましょう。まずは、1種類の和音の三角形から正二十面体を作ることができるか見てみます。図のように、ある面にドミソの三角形を貼り、ドの点を中心として、反時計回りにドミソの三角形を次々に貼っていくと、最後に「ドミミ」という面ができてしまい、1種類の和音の三角形では正二十面体が作れないことがわかります。

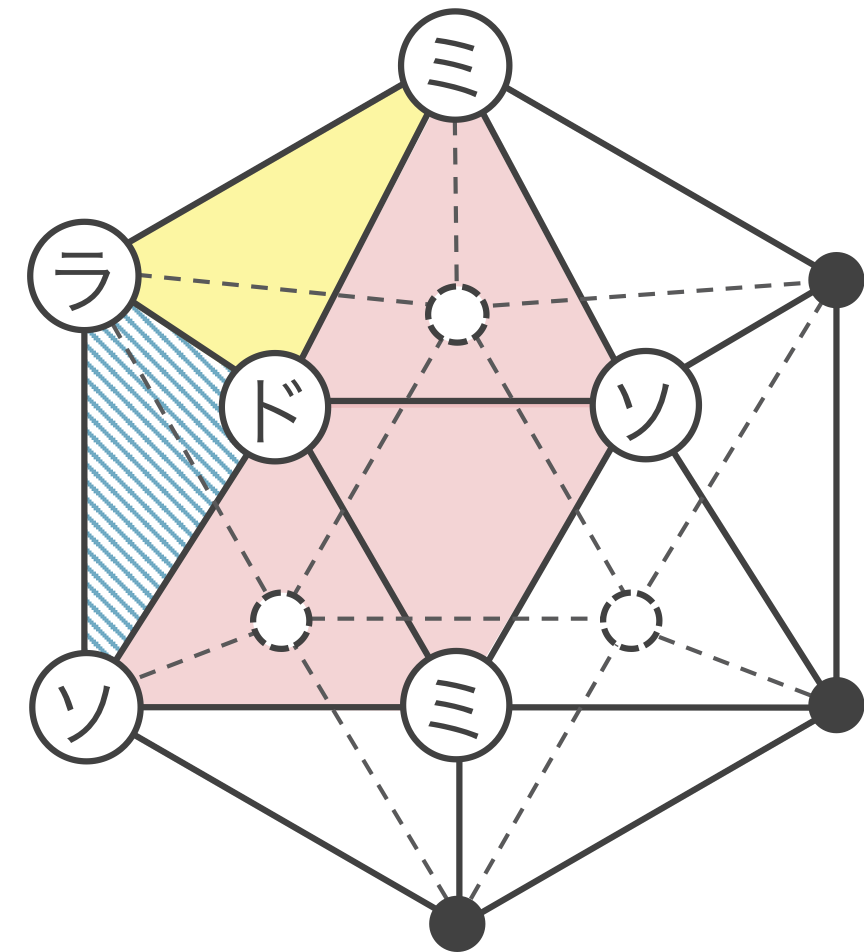
では、2種類以上の和音の三角形を使えば正二十面体は作れるのでしょうか？実際、下図のようにラドミの三角形を使うと、「ドラソ」という7種類の和音には含まれない3つの音が出てきてしまい、2種類以上の和音の三角形を使っても正二十面体は作れないことがわかりました。

正二十面体が和音の三角形で作れない理由は、頂点から出ている辺の本数の偶奇性と非常に深い関係があります。実際、正八面体においてはどの頂点からも偶数本の辺が、正二十面体では奇数本の辺が出ています。この偶奇性に着目することで、正八面体と正二十面体だけでなく、凸多面体と呼ばれる図形全体に対して、次のような定理を得ることができました。

定理 (大野、2015)
すべての面が三角形になっている凸多面体が和音の三角形で構成できるための必要十分条件は、凸多面体の頂点に接続している辺の本数がすべて偶数本であることである。

 

今回は7種類の音を組み合わせて和音の三角形を構成し、それらを使ってどのような図形を作ることができるのかについて考えましたが、私はその問題を「グラフ理論」という数学の分野の言葉を使って一般化しました。そして、今回は詳細を省略しますが、被覆空間や基本群といった代数的トポロジーを使うことで、ひとつのまとまった理論を構築することに成功しています。

私は2017年にスロバキアの国際研究集会に参加し、上記の定理や理論について発表をしました。その際、多くの海外の研究者と研究について議論を交わし、数学を通じて世界と繋がる体験をすることができました。また、この研究集会には色々な国から女性数学者も出席しており、彼女達との交流を通して女性の研究者が世界でも活躍していることを身をもって実感できました。

 

 

 

 

 

 

 

 

 

 

 

参考文献
根上生也編、「数学活用」、啓林館

※2019年7月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。