2017年9月10日および2018年2月17日、第二回数理女子ワークショップ第１・２弾の開催レポートの後編です。
前半の様子はこちら

ランチ後はまず座談会です！

第1弾の座談会では、佐々田先生（東京大学）ファシリテーションのもと、数学者の前島信先生（慶應義塾大学名誉教授）と嶽村智子先生（奈良女子大学）、中島さち子先生（音楽家）、近藤宏樹先生（高校数学教諭、元アクチュアリ）に、お話いただきました。「確率」や「偶然」について、また「数学」について、数学を専門にしている方々であっても感じ方は人それぞれ！多彩な「数学観」を楽しみました。

第2弾の座談会では、中島先生ファシリテーションのもと、田中泰生さん（ゲーム会社社長）、山羽教文さん（スポーツ関連会社経営者）、池田純さん（ラグビースクール経営者）、佐々田先生（数学者）でお話いただきました。スポーツでも確率を練習や戦略に利用していること、ゲームではレアキャラ出現確率などを綿密に計算していること、「確率」と「統計」の研究の違いなどが語られました。

その後は親子一緒に「針金投げゲーム」！

まず、5cm間隔で横線を引いた模造紙を準備します。また、10cm, 15.7cm, 20cm, 30cm のまっすぐな針金を準備し、各自好きな長さのものを選びます。そして選んだ針金を上から模造紙に落とし、何本の横線と交わったかを数え、記録します。

記録報告が終わったら、次に針金を（立体的にならないように）自由に曲げてオリジナルな形を作ってから模造紙に落とし、横線と交わった個数を数え、記録・報告します。

黒板にどんどん描かれる数字。

「10cmのまっすぐ/10cmの曲線/15.7cmのまっすぐ/15.7cmの曲線/20cmのまっすぐ/20cmの曲線/30cmのまっすぐ/30cm の曲線」ごとに分けて「横線と交わった個数（と曲線の概形）」が描かれていきます。

「さて、何か気づいたことはありませんか？」

聞いてみると、素晴らしい発見がどんどん返ってきました！

1) 針金の長さが長いほど、交点の数は増える

2) 曲線の方が交点は少なくなっているように見えるけど、時々すごく多いのもある

3) 曲線で交点が少ないのは、立体的に浮いてしまったからかも？すごく多いのはこんなウネウネ曲線がちょうど直線に乗ったとき？

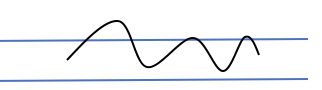
長さと形が同じ組み合わせごとに、横線と交わった個数の平均値を出して、さらに考察を深めていきます。

4) 針金が20cmの場合の平均値は針金が10cmの場合の平均値の２倍くらいになっている！

5) 針金が30cmの場合の平均値は針金が10cmの場合の平均値の3倍くらいになっている！

6) 針金の長さが同じならば、平均値は、まっすぐな場合と曲がっている場合はそれほど変わらない

ということで、皆さんの実験からオリジナル予想が２つ立ちました！

【予想１】　交点の数は針金の長さに比例する

【予想２】　交点の数はまっすぐでも曲がっていても変わらない

「では、直径5cmの円形の針金の場合はどうでしょう？」

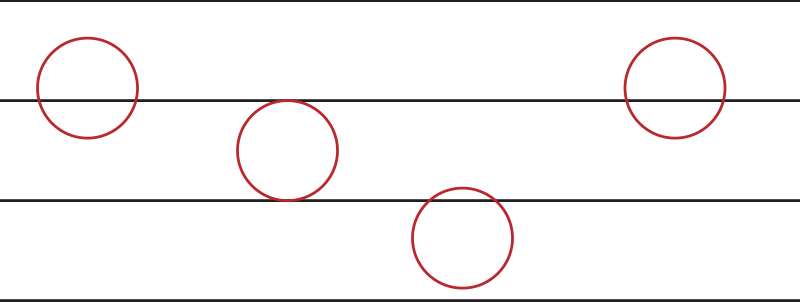
上記のように、どう落としても、必ず２個になります！

直径5cmの円の長さは円周率πとすると5πcm、つまり約5×3.14=15.7 cm です。つまり、5πcmの針金を投げると必ず2つの交点を持つことがわかりました。実際の実験でも、15.7 cmの針金の場合の平均値は確かにほぼ２になっていました。

実は、このことと、実験から導いたオリジナル予想を組み合わせると、次のようなビュフォンの針と呼ばれる有名な問題の答えを求めることができます。

「5cm間隔で横線を引いた模造紙に、長さ5cmの針を落としたら、横線と交わる確率はいくつでしょうか？」

オリジナル予想を使えば、5cmの針金を投げたときの交点の平均値（横線と交わる確率）は、以下のはずです。

2×5÷5π=2/π

このビュフォンの針の問題は、積分や三角関数など難しい数学を用いて計算できます。が、今回は、実験から導いたオリジナル予想のおかげでとても簡単に計算できました！

しかし、針金を投げるだけの実験に、なんで突然円周率πが現れたのでしょう？とても不思議ですね。

数学では、このように全然違うように見える2つのことが神秘的に繋がっている！ということに気が付くことがあります。ぜひ、この不思議をじっくり味わってみて下さい。また、オリジナル予想が本当に正しいのかどうかについても色々と考えてみてください。

休憩をはさんで再び親子別々の部屋にわかれてから、お待ちかねの「創作コーナー」。ここは、子どもたちが特にイキイキする時間。

今回は、確率の考え方を生かしながらグループごとに、学校のお祭り用のゲームや占いを創る！というお題に挑戦しました。

後ろの机にはトランプやシールや囲碁盤、紙、ボール、テープ、サイコロなどなど、さまざまなグッズが揃っていて、早いもの順でどんどん取っていきます。

創作の時間も第１、２弾共に大いに盛り上がりました。TAも混じって皆で協力しながらアイディアを出していきます。ゲームや占いを面白くしようと考えているうちに、勝ち・当たりをどれくらい少なくすればよいか、どの程度の景品が適当か、など考えはじめ、確率計算を始めるグループも多数。完成したら、作ったゲームや占いの説明と確率的考察を書いた２枚の模造紙と素敵な作品をもって、親子全員で同じ部屋へ集合。

 

テーマは学校のお祭り！ということで、各グループお店屋さんとお客さんの２班に分かれて実際にお祭りを楽しみました。10-15分程度で交代して皆十分満喫したところで終了。

大人気で混んでいるお店なのに元気いっぱいに呼び込みを続ける女の子、午前中に行ったサイコロゲームを発展させた数学者を唸らせるようなゲームや、お母さん目線の素敵な占いなどもあり、非常に賑やかな時間になりました。

最後はみんなでゲームや占いの工夫した点や今日一日の感想を共有し、全体写真をとって終了。長いようで、あっという間の1日でした！

以下、終了後にいただいた感想の一部を紹介します。

「数学は、一つの答えを導き出す物だと思っていましたが、それだけではなくスポーツやゲームなどにも、深くかかわっている事におどろきました。」

「針金ゲームの確率と円周率の関係がびっくりしました！」

「机の上のお勉強と思っていた数学でしたが、世の中にたくさんあふれていることを知ることができました」

「ふだんは遠い存在だった数学・算数が少し身近に感じました」

「憂うつだった算数の時間が、（今後は）楽しくすごせそうです。」

「難しいことをしらなくても地道にこれはどうかな？あれは？と考えていくといろいろなことがわかるのがおもしろかったです」

「計算でわりきれないことはいっぱいあるでしょと思っていましたが、意外と数学の世界もわりきれないものなんだなと人の体温を感じました」

「座談会の拡大版をぜひ…!! とっても面白かったです。」

「シリーズ化して下さい！！大人女子のみもぜひ！！」

数理女子ワークショップは毎回、たくさんの社会人や大学院生、大学生にスタッフとして協力いただいています。スタッフからの感想も一部ご紹介します。

「参加者の方々の自由な発想にふれられて，こちらとしても面白かった。

参加者の方々もみな楽しそうにゲームの作成，紹介，体験をしていたのが印象的だった」

「スタッフ同士でも出会いや発見があってとても有意義な一日でした。」

「全体として楽しんでいただけたのが何よりだった．お母さんに主体的に作業してもらうという形態は今後も続けた方がいいと思う。」

「親子が別々の部屋で同じ内容を考えるということは、とても面白いと思う！今後も楽しみです。」

「間違いを気にせず自由に考えられる雰囲気があり、参加者の方々に楽しんでもらえていたと思う。」

「やはり、お子さん、お母さんの笑顔にはやる気をもらいます！」

自由で創造的で楽しい算数・数学の世界を少しでも体感いただけたならば、スタッフ一同とても幸せです。

Webサイト「数理女子」では、今後も、さまざまな角度から算数・数学の魅力をお伝えすると同時に、魅力をより直接的に体感いただけるようにワークショップなども開催していきたいと思います。今後ともどうぞ何卒よろしくお願いいたします。

 

数理女子ワークショップ講師・スタッフ一同

 

 

 

※2018年8月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。

写真：河野裕昭氏撮影