博士論文とは、大学卒業後、大学院の修士課程を修了し、さらに博士課程へ進んで研究した内容をまとめたものです。難しい言葉もたくさんあります。わからないことだらけでも全く大丈夫！！研究の雰囲気や、数学の世界にどんな分野やテーマがあるのか感じてもらえればと思います。研究者同士でも、お互いの博士論文の内容はなかなか理解できるものではありません。実はわからないことって面白いことの始まりです。存分に楽しんでください♪

論文題目「Stability and instability of standing waves for nonlinear Schrödinger equations」
(東北大学理学研究科数学専攻にて取得。)

波の伝播する様子を調べるためには、定常波、定在波、進行波などの特殊解の存在および安定性^*1の解析が重要な役割を果たします。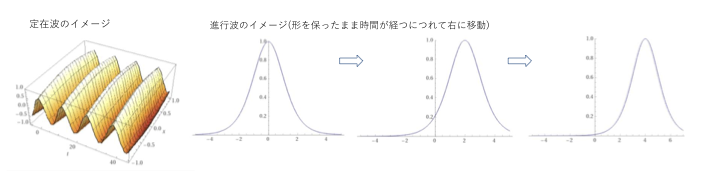
物理的には、波動現象^*2において初期値状態に関わらず、時間が経てば同じようなパターンの波が観測でき、それが上記の波のうち安定なものによって記述されているのではないかという考え方に基づくものです。このような観点に立って、国内外で物理的にも数学的にもそれらの波の存在や、安定性に関わる多くの研究がなされています。非線形 Schrödinger 方程式は非線形光学やプラズマ物理などのモデル方程式として現れる波を記述する方程式であり、定在波の軌道安定性については1980年代に完全に調べられ分かっています。その後、これらの結果は、非線形 Klein-Gordon 方程式などを含む抽象的なハミルトン系^*3に対する孤立波解^*4の安定性に関する一般論として Grillakis-Shatah-Strauss の論文にまとめられました。しかし、現象をモデリングする際に非線形近似を高次まで展開したり、媒質の効果を取り入れて非斉次項を取り込むと、方程式にはスケール不変性^*5がなくなり、Grillakis-Shatah-Strauss の一般論における安定性及び不安定性に関する十分条件を直接確かめるのが困難となり、様々な工夫が必要になります。私が博士課程の学生であった頃、希薄原子気体でのBose-Einstein 凝縮体の実験による捕獲成功でアメリカの二つのグループがノーベル賞を受賞し話題となっていました。その凝縮体の振舞いは調和ポテンシャルを伴う非線形 Schrödinger 方程式でモデリングされるといいます。

つまり Grillakis-Shatah-Strauss の一般論が直接適用できない例であり、さらに当時最新の物理を表現するモデルに出会ったのです。そこで、私はそのBose-Einstein 凝縮の方程式における定在波解の安定性について研究を始め、調和ポテンシャルを伴うことで、これまで定在波解が不安定であった場合でも安定化することがある、という事実を初めて厳密に証明しました。この成果により日本数学会建部賢弘奨励賞をいただきました。

学生の頃は、同じ研究室に所属していた先輩・後輩に助けてもらい、多くのことを学びました。良く出来る先輩たちを見ながら自分の能力にもどかしさを感じ続け、とても悔しい思いをしました。私の分野は私が学生の頃に Bourgain (1994年フィールズ賞) や Tao (2006年フィールズ賞) の活躍もあり全盛期で、指導教官が積極的に世界のトップで活躍している研究者を仙台に招聘してくれ、非常に刺激になりました。違う分野の研究室の同級生たちとも、車で美味しいものを食べに行ったり、一緒に温泉に行ったり、発表をお互いに聞きあって意見を言い合ったりと、今となっては良い思い出であり、同期が研究者として現在でも活躍している姿をみて誇りに思います。

*1「安定性」波をどんな方向から揺らしても形が崩れずに保たれることを安定といい、その逆に形が崩れたら不安定という。

*2「波動現象」媒質内の変化が次々と媒質中を伝わっていく現象

*3「ハミルトン系」ハミルトニアンと呼ばれる関数から定まる、ニュートンの運動方程式を一般化した運動方程式

*4「孤立波解」ただ一つの山だけが伝わっていく波

*5「スケール不変性」長さやエネルギー、その他の量を表す変数に共通の係数をかけても変化しないという性質

※2022年10月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。