数学って、無味乾燥な数や文字や式をごちゃごちゃいじりまわしているだけで、まるで面白くない、だいたいなんだかひどく細かいけれど、こんなちまちましたことから何か新しいことが出てくるの？と感じている人も、数や式や文字を操るなんてお茶の子さいさい、数学なら得意中の得意だし、きちんと細かく考えることもばっちり、という人も「へえ！」と感心すること請け合いの一冊が、ここにあります。
今から題名と著者をお教えしますので、とにかく手にとってみてください。

「数学のできる人はこう考える」、シャーマン・スタイン。

シャーマン・スタイン著『数学ができる人はこう考える』白揚社（2003年 4月 ）

突然そんなことをいわれても……。確かにそうですね。では今から少しだけ、わたしのおしゃべりにおつきあいください。　

その１　数や文字や式の操作＝数学ではない。
　数学は、人類が物を勘定したり測量しはじめたときに生まれたとされています。つまり5000年以上の歴史があるのですが、今の形の文字や式が最初に登場したのは16世紀で、まだ500年も経っていません。もちろん文字や式は数学にとってたいへん強力で便利なもの、いわば「鬼の金棒」のような存在ですが、それが数学のすべてではありません。数学的な思考こそが、数学なのです。

その２　ひどく細かいからこそ、想像もしていなかった新しいことがわかる。
　数学が一つ一つの手順を細かく慎重に重ねていくのにはわけがあります。なぜなら数学的な思考は日常の現実から離陸するため、とことん信頼できるやり方をしておかないと、あらぬ方向に飛んでいってしまう危険があるからです。数学的な思考は科学のもっとも強力な武器であり、科学は現代社会の基本になっています。ですから数学があらぬ方向に飛んでいくと、社会全体がめちゃくちゃになってしまいます。（さらに、現実から離陸するからこそ、現実のなかでの経験年数、つまり年を取っているかどうかとは無関係に、中学生でもちゃんと数学的な思考ができる。したがって、大人がいうことだから正しいと思う必要はなく、時には大人と対等に渡り合うことができるのです。）

さらに数学は、絶対確実な思考を積み重ねることによって、日常の現実に縛られているわたしたちが想像もしていなかった新たな事実を教えてくれます。そのような数学の醍醐味をぜひ味わってみてほしい！というのがこの本の著者の願いです。 この本では、「スポーツで接戦の末に最後に続けて二回勝ったほうが勝つ場合、同点から勝負がつくまでに何回勝ち負けが繰り返されそうか」とか、「二人の候補がいる選挙で最終的に勝った候補が最初から最後までリードし続ける可能性はどれくらいか」、あるいは「無数の平行線の上に棒を落としたときに棒が線と交わる可能性はどれくらいか」といった現実のなかの問題が取り上げられています。

ところが、たとえば最後に紹介した「床に平行な割れ目が何本も走っている部屋で棒を一本投げるとする。一人のギャンブラーは棒がどの割れ目とも交わらないほうに賭け、もう一人が割れ目のどれかと交わるほうに賭けるとき、この二人の勝率はそれぞれいくらか（棒の代わりに針や頭の取れたピンを使ってもよい）」という「ビュッフォンの針の問題」からは

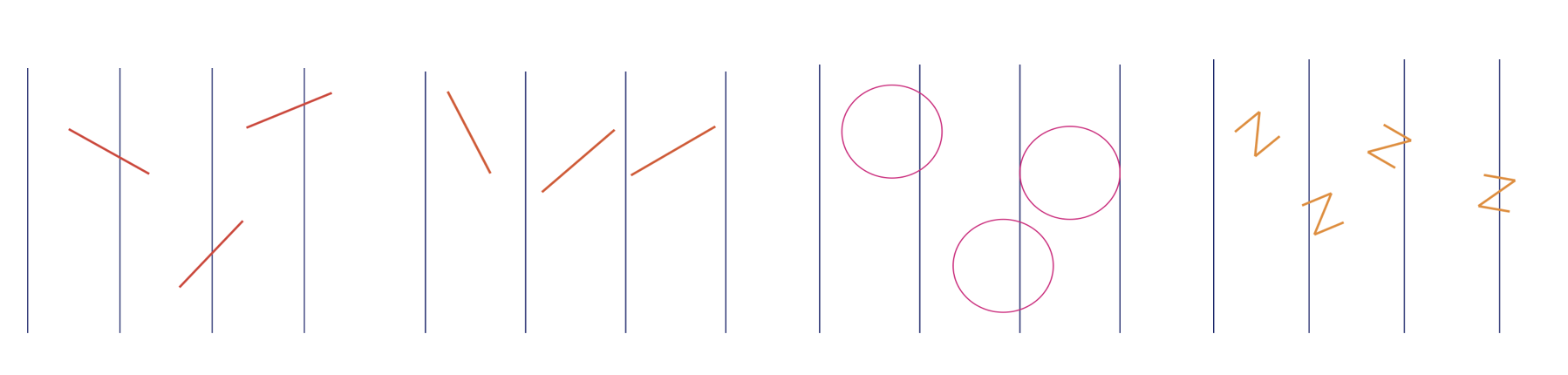
①棒（針）と平行線が交わる確率という元々の問題を針と線の交点の数の問題に読み替えて（視点の変換）
②針の形がいろいろである場合にどうなるかというふうに問題を広げて（一般化）
②何が交点の数を左右しそうかを考え（分析的な思考）
③簡単な実験をしてみて（実際の試行）
④さらに架空の虫の助けを借りて実験結果を確認し（思考実験による推論）
⑤最後にきわめて特殊な針（？）を考えること（特殊化）によって意外な答えが得られるのです。（その答えが何なのかは、読んでみてのお楽しみ。）

かと思えば、候補が二人の場合の選挙の問題が図形の問題に化けてみたり……。これらはすべて現役の数学者たちが駆使する数学的思考の典型であって、正統派の数学的思考といえます。それでいて中学生にも理解できて、数学のエッセンスに触れることができる。ですから数学が面白いと感じている方もそうでない方も、どうかこの本で、数学がもたらす「不思議」を味わってみてください。

※2018年10月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。