大空を羽ばたく鳥の群れ、海を泳ぎ回る魚の群れ、地上を歩く小さな虫の集団。周りを見渡してみると（あるいはインターネットで動画を検索してみると）、群れを作って行動する生き物がたくさんいることがわかります。群れの様子を眺めているだけでも楽しいですが、素朴な疑問も思い浮かぶかもしれません。例えば、単独で行動せずに群れを作ることのメリットは？誰の指示もなしに群れができるメカニズムは？

群れを作るメカニズムを解明するため、物理の考え方や数学の方法を使った研究が盛んに進められています。そのような研究分野はアクティブマター物理学と呼ばれ、比較的新しい研究分野です。アクティブマターは「動くもの」という意味で、普通の物質のように自分では動かないものと対比するために使われる用語です。アクティブマターの研究は、生き物の集団などを観測して動きのルールを推定する観測・実験研究と、一定のルールに従う集団を数学で表現したもの（数理モデル）を調べる理論研究に大別されます。

ここでは、ビチェックモデルと呼ばれる、単純化された群れの数理モデルを紹介します。ビチェックモデルでは、動く粒子の集団を考え、各粒子は①一定の速さで動く・②たまに動きの向きがぶれる（乱雑さ）・③近くの粒子と向きを合わせる（協調性）というルールを設定します。これら三つのルールを数学で表現し、粒子集団の動きをコンピュータで調べると、粒子全体が示し合わせたかのように同じ向きに動き出すことがわかります。群れを率いるリーダーがいなくても、協調性があれば集団運動が可能になるのです。このようにコンピュータを使って数理モデルを調べることは、数値実験や数値シミュレーションと呼ばれます。

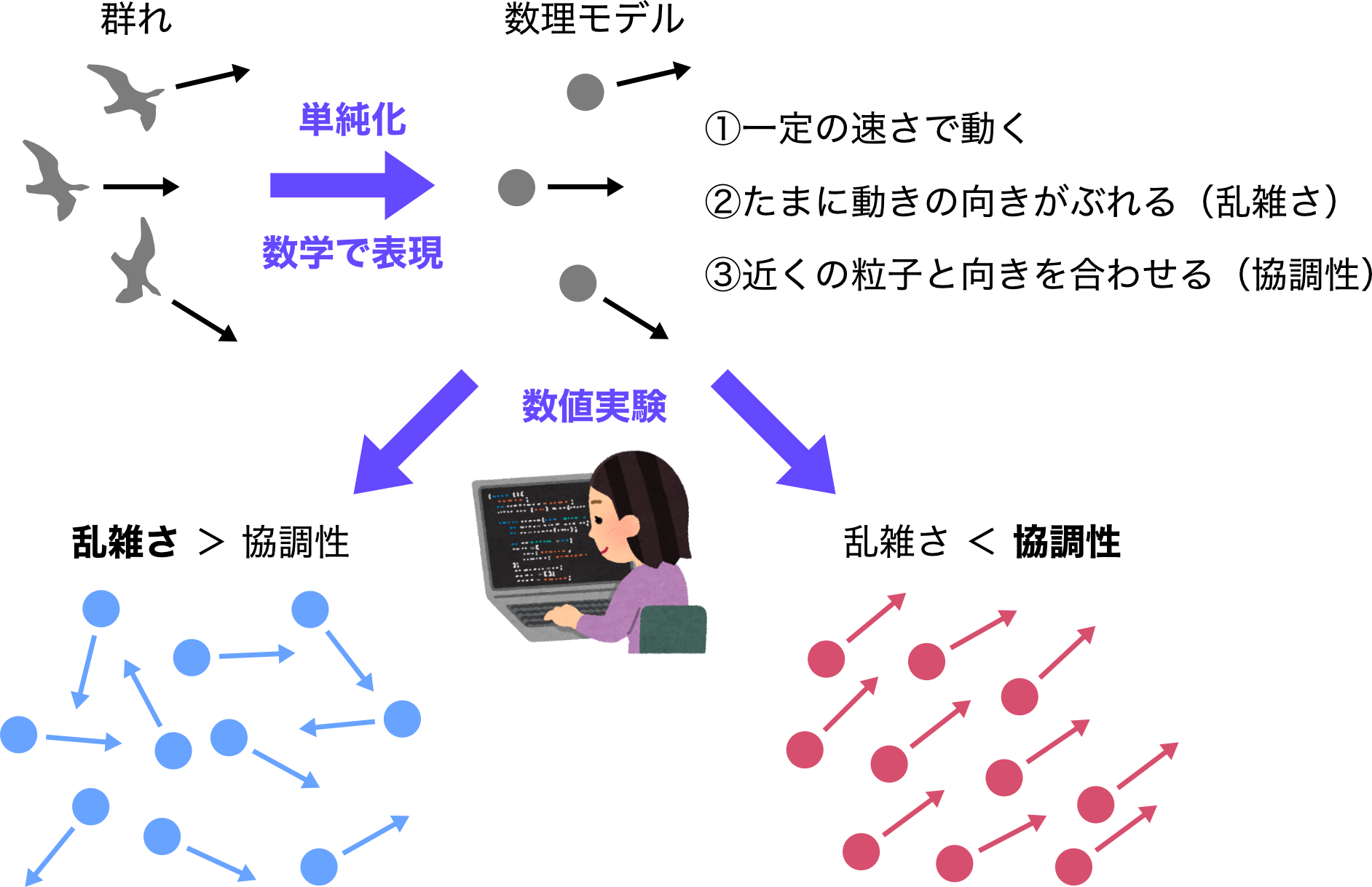
数値実験のメリットは、数理モデルのパラメータ（ビチェックモデルの場合は粒子の速さ・動きの乱雑さ・協調性の強さ）を、スライダーバーを動かすように自由に調整できることです。例えば、協調性を強めたり弱めたりして粒子集団の動きの変化を見ることで、集団運動にとって協調性がどれくらい重要なのかを調べることができます。数値実験の結果によると、協調性と乱雑さは互いにライバル関係にあり、協調性が乱雑さに打ち勝った場合にのみ集団運動が可能となります。

数理モデルでは、ビチェックモデルで設定したルールのように、思い切った単純化がしばしば行われます。これは、集団運動などの現象にとって主要な要素以外をそぎ落とすことで、必要最小限のメカニズムを調べるためです。一方で、実世界の群れの動きを説明するためには、観測・実験データを使って数理モデルの単純化の妥当性を検証し、必要に応じて数理モデルをアップデートしていくことも大切です。例えば、ローマで観測された千羽ほどのムクドリの群れでは、協調性のルールがビチェックモデルとは異なっており、個体間の距離が遠くなっても協調性の強さがあまり変化しないと考えられています。このルールを取り入れると、敵からの攻撃に対して群れがより安定して存在できることが数値実験により示されています。

私は、大学院では物質を対象にした物性物理学を専攻しており、アクティブマターという分野を本格的に知るようになったのは大学院を卒業して研究員として働き始めてからでした。自分で色々と数値実験をしてみたり、群れの野外観察の論文を読んだりしてアクティブマターの面白さに触れ、徐々に研究にのめり込んでいきました。現在、物性物理学の研究で学んだことを活かし、量子力学に従うようなナノメートル（10億分の1メートル）スケールの粒子も群れを作ることができるのか？という問題に数理モデルを使って取り組んでいます。数学という共通言語を使うことで、分野の垣根を越えてアイデアや概念を拡張していく楽しさは理論研究の醍醐味の一つだと思います。

※2023年12月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。