■生き物と数と私
私は小さい頃、「暗算好きの昆虫少年」でした。昆虫を捕まえて図鑑で名前を調べ、飼育してスケッチし、最期を見届ける。はたまた、走る車のナンバー（たとえば12-34）を見て、二桁×二桁の暗算（12×34=408）をする。そんな幼少期を過ごしました。

京都大学の理学部へ入学したのは、生物・数学・化学・物理、いろいろ勉強したかったからです。特に夢中になったのは、ε-δ論法を始めとする抽象的な数学でした。もちろん難解でしたが、抽象的な思考を行なうこと、そして具体的に計算する技術を身につけることを楽しみました。

一方で、相変わらずの生き物好きでもありました。野外実習で草木や昆虫に触れることは、実に楽しい体験でした。しかしどうしても、数学と生き物への思いを両立することは困難に思えました。これらは切り離されていていつかはどちらかを諦めねばならないという、「いずれ確実におとずれる失恋」への強い悲しみに憔悴し、体調を崩してすらいました。

大学一年生の秋。フットサルで腰の怪我を負った私は、図書館に通い始めました。大学の図書館って、実に魅力的なんです…！数え切れぬほどの、魔導書のようにボロボロな本。それらを一日中むさぼり読める、広い空間。毎日のように通って、数学・物理学・生物学の本を手に取り、夢中で読みました。

■数理生物学との運命の出会い
図書館に足繁く通う、そんなある日。「数理生物学入門」（巌佐庸 著）という本を図書館で発見しました。心臓の鼓動が止まらなくなった興奮を、いまでも覚えています（止まっては困ります）。「簡単な数学で、生き物の複雑さを、かくも表現できるのか！」と感動してあっというまに読み切りました。そして、「数学と生き物を愛する自分が、これからの人生、どこに向かうか？それは、数理生物学だ！」と決断しました。著者である巌佐先生に電子メールで相談し、先生の当時おられた九州大学で修士課程に進み、数理生物学の研究を行なうことを決意しました。ちなみに両親に、京都大学から九州大学の大学院へ進学する意志を、反対されやしないかとドキドキしながら伝えたときの反応は、「え〜！いいなぁ！」というものでした。私が挑戦したい研究への志を、ただただ純粋に応援してくれる、そのシンプルな言葉に心の底から救われたのを、いまでもよく覚えています。ただし、会話を続けるなかで、その言葉の真意が「え〜！福岡はご飯が美味しい街だ！いいなぁ！」だったと判明しました。ま、結果オーライ。

■数学で生物学：モデルとは何だろう？
さて、そんな形で私が選んだ「数理生物学」という分野では、数理モデリングという作業が行なわれます。これは、我々が現象（例：タンポポの種子が飛んだ）を認識して、それを数式で表現すること（例：「種子の飛んだ距離は平均Xメートルとする」）です。現象やその認識自体は、他者に100%正しく共有できないけれど、それを100%正しくはなくても表現する数式そのものは100%正しく共有できますし、数式であればその性質を詳しく調べることができます（図1）。

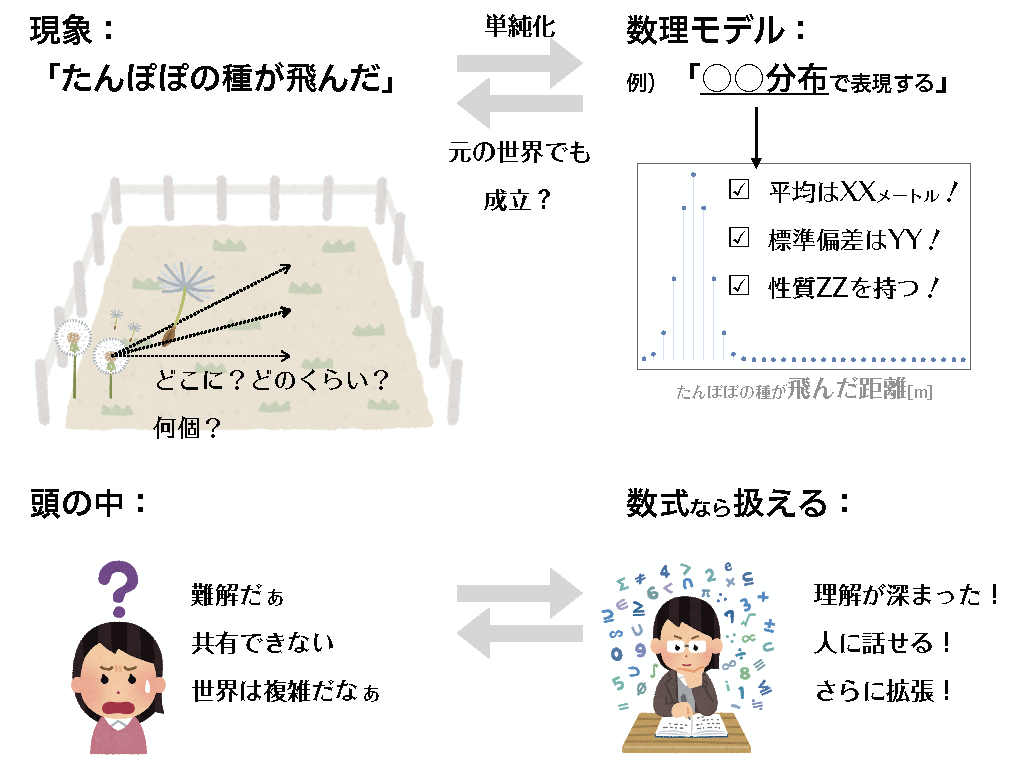
図１

そして、そうして導かれた性質も、現象の中に内包されているものであることが期待されます。

性質を知りたい「生物の現実」は複雑で難しい。そこで、よく知っている数式の世界で現象の代わりになるもの（モデル）を表現して、その世界でモデルの性質を調べ、もとの複雑な現象世界に戻してあげるのです。数理モデルを運用する科学分野は、時として「数理科学」と言われます。

■あなたもモデルを使っている
科学におけるモデル、と耳にすると、難しく感じるかもしれません。しかし、みなさんも無意識にモデルを利用しています。たとえば仕事や勉強において、複雑な処理・操作・概念・手続き等を耳にしたとき、「わかりやすい具体例が知りたい」、「実際にやって見せて欲しい」と感じることがあると思います。それは、もとの複雑な世界から、「具体例」というわかりやすいモノ（モデル）を切り取ってくることです。つまりモデリングです。人の脳みそは複雑な世界を100%正しく認識できませんから、モデルを作って脳内で理解しているのです。

■生物の数理モデル
ここで私が研究で用いる数理モデルの具体例を話すには、進化ゲーム理論の概念や、「どのような性質を引き起こす遺伝子がたくさん子どもを残せるか？」という考え方（自然淘汰の概念）を説明する必要がでてきてしまいます。今回は、それはしません。ごめんなさい。そのかわり、次のようなトピックをご提供します。数理モデルで、以下のような問題を考察できることって、すごくないですか？：

• 【なぜ生き物は移動する？】なぜタンポポの種子には綿毛があるのか？種子を飛ばすと、途中で死亡するかもしれないのに！…
  【数理モデルで導かれる答え：】タンポポの種子に綿毛が無い場合、その種子は親個体の文字通り根本に落ちるだろう。すると種子たちは（母親を共通とする）「きょうだい」なので、資源をめぐって競争することになる。そんな状況で、種子をちょっとだけ飛ばす遺伝子を持つ個体が登場すると、そのちょっと飛んだ種子は（生き残って、どこかの土地に定着したら）「きょうだい」同士の競争を経験しないので、次世代にたくさん遺伝子を残せる（Hamilton & May 1977）。そして更に、「まわりに他の種子がいないような空き地」にも種子を定着させて、資源をひとりじめできて、次世代にたくさん子供を残せるだろう。「ちょっと移動する」というのは割合であり数値であるから、数理モデルで表現できる。
• 【卵子と精子：なぜ非対称な関係？】なぜ、多くの生物では「精子（オスの配偶子；小さい）」と「卵子（メスの配偶子；大きい）」という非対称性が存在するのか？…
• 【数理モデルで導かれる答え：】もともとは同じくらいの大きさの配偶子同士が接合するシステムであった。しかし配偶子を分裂させて、（生存率は低いが）小さい配偶子を生み出す「倍賭け」遺伝子Xが突然変異により登場すると、そのような遺伝子を持つ配偶子から多くの子孫が次世代に残り、次世代は小型配偶子（オス配偶子）を生み出す遺伝子を持つ個体が増える；そのような状況で、栄養を確保しておける大きい配偶子（メス配偶子）を生み出す遺伝子Yが突然変異で登場すると、小さい配偶子よりも生存率が高いので、そのような遺伝子をもつ個体が次世代に増える。このプロセスは「分裂回数」などの数字が伴うので、数理モデルで表現できる（図2）。

   

  

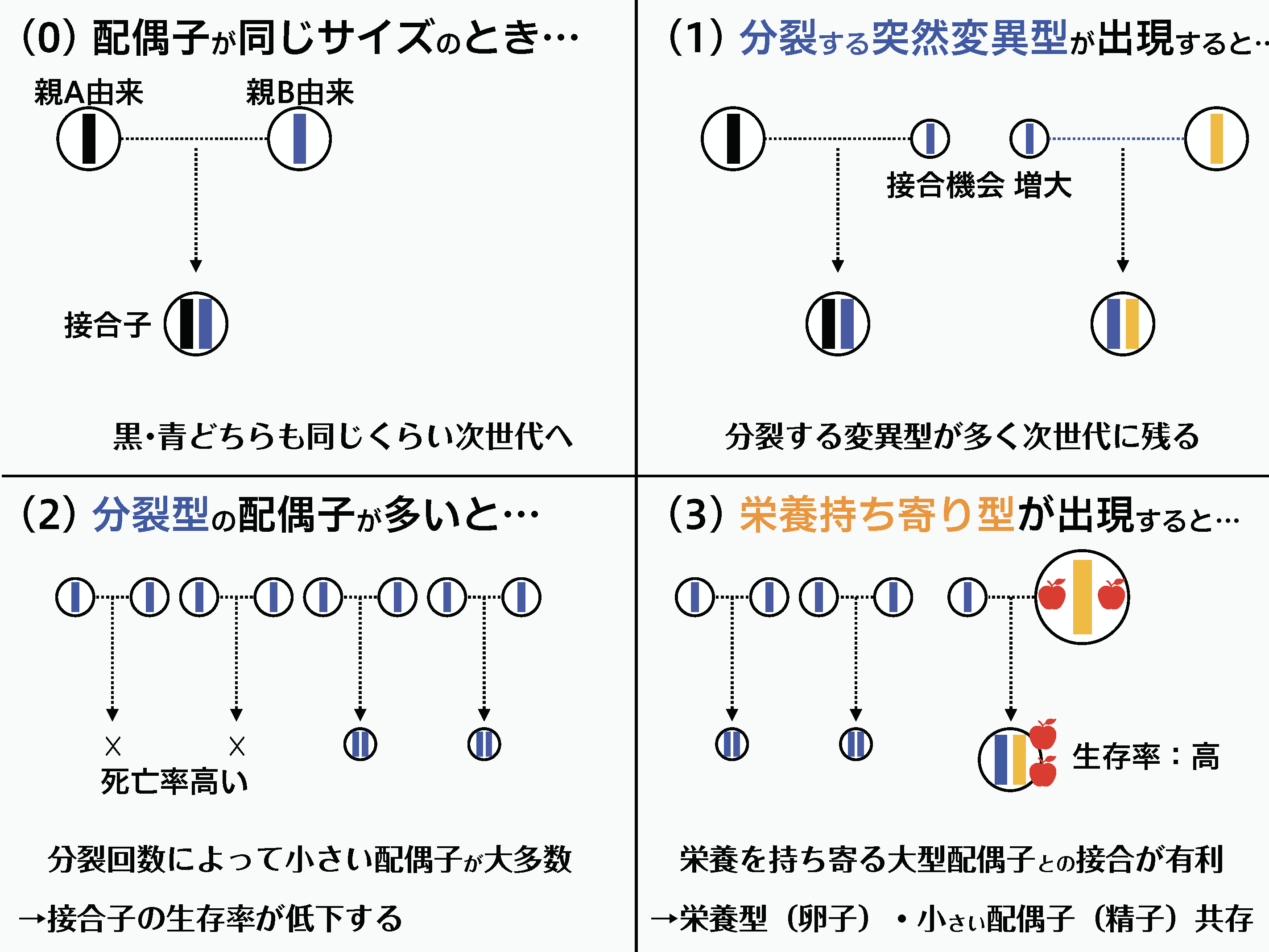
  図２ ：

「働きアリは、自身では繁殖できないのに、どうして女王アリのために働くのか？」、「どうして多くの生物の性比は１：１なのか？どうしてそうでない生物もいるのか？」、「どうして病気に伴う死亡率は、若い個体と成熟した個体とで異なることが多いのか？」、といった問題に答えることも可能である。

上で述べた例は骨子だけですが、数理モデルを用いて生物現象を表現すると、数理モデルがない段階と比べて、「生き物への理解が進んだ」ことになります。もちろん、すべての数理モデルは、100%正しく現象を反映していないので、「誤り」です。しかし、そもそも現象を全員が正しく認識・共有できている保証はありませんから、全員が正しく認識・共有できる数式を表現・理解することで、客観的に現象を理解することに繋がるのです。これによって、「みんなが共有できる考え方、議論の材料、現象の理解の助けとなる客観的考察」を、数理科学は提供してくれます。

■まとめ
「生き物も算数も大好き！」そんな気持ちが両立する世界が、数理生物学にはありました。あなたが夢中になるどんな分野（科目）の間にも、必ず共通点があります。そしてそれら共通点さえ見つかれば、数理モデルで表現して議論できる場合がほとんどです。科学の世界の広がりは、無限です。

本稿を読まれた皆さんには、男女も年齢も忘れて、大好きなこと・夢中になれること・ワクワクすることを、思う存分、学び楽しんで欲しいです。競争意識なく夢中になれるものがある人生は、それだけでも素晴らしいものです。

そして周りの方々には、そんな姿勢を、たとえば昆虫採集と暗算が趣味の少年少女がいても、「変」、「おかしい」、「非常識」といった、個性を抑圧してしまう言葉をかけるのではなく、温かく応援し、育ててあげて欲しいです。

私は、京都大学を卒業してからは、福岡、フランスはモンペリエ、スイスはローザンヌ、アメリカはカリフォルニア、と、いろいろな土地に住みました。辛いこともたくさんありました。でも、どこで生きようとも、常に数学を学び楽しむ主体性、そして家族・友人・研究者たちとの関係性が、私を常に元気づけ、私を育ててくれました。この経験なくして、きっと今の私という研究者は、存在し得なかったでしょう。私はこれからも、一生研究と勉強を続けますし、「なにかを学び続けたい」姿勢を持つ人々のことを、心の底から、応援し続けます。

数理生物学者としての私は、多くの方々に支えられてきました。「数理女子」への本寄稿は、数学の楽しさを私に教えてくださった恩師である、黒谷和民先生に、捧げたいと思います。

注釈
図１：モデルのイメージ。「たんぽぽの種が飛んだ」という現象そのものは認識できても、どのくらいの種子がどれくらいの距離飛んだのかは、とても複雑であり、頭の中では整理できない。しかし、数理モデルを用いて、「たんぽぽの種が飛ぶ距離」を表す関数（分布）を数式で表現すると、その分布が満たす性質を調べることで、種の飛ぶ現象への理解が深まる。

図２：精子と卵子が自然淘汰によって共存する原理。自然淘汰は、どういう遺伝子が次世代に残りやすいかを決定する。

※2021年2月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。