ご存知の通り「折り紙」は、日本に古くから伝わる紙を使った遊びの１つです。
みなさんも幼稚園や小学校に通っていたころには、色の付いた正方形の紙を折って鶴や小鳥、舟やヤッコさんなど、さまざまな形を作ったことがあることでしょう。
その一方で、折り紙は小さな子供の遊びという印象が強いため、中学、高校へと進学するうちに、折り紙に触れる機会はなくなってきているのではないでしょうか。
でも折り紙の世界はとても広く奥深いものです。「大人になったから興味ない」ではもったいない！
私は大学での研究の一環で、紙を折って作ることができる形の研究をしています。１枚の紙を折るだけでも驚くほど表現豊かな形を作り出すことができ、大学の教員になった今でも、１枚の紙から作られる造形と、そこに表れる予想外の陰影の美しさにワクワクすることがあります。

折り紙と図形問題
みなさんは中学や高校で図形の学習をする中で、下図の「四角形を対角線で折り返してできる図形」に含まれる三角形の性質を問うような、折り紙の性質を使った問題に遭遇したことがあると思います。

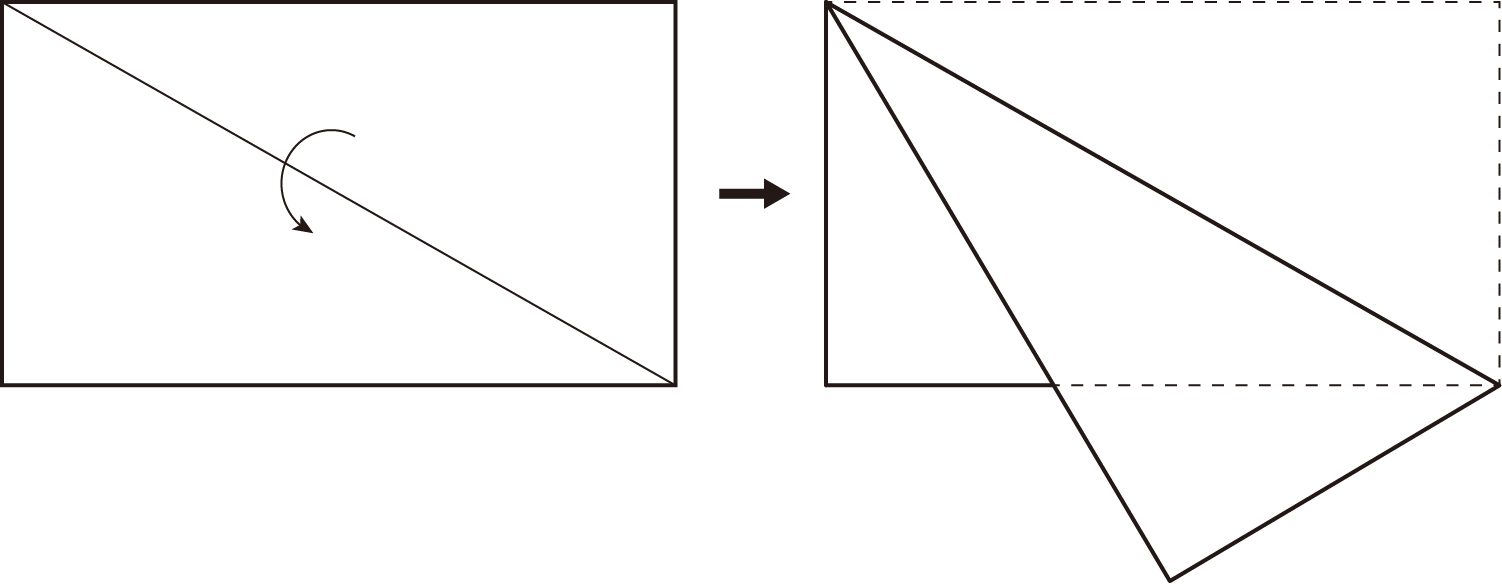
「紙を折る」という操作は、折り線によって「点と点を線で結ぶ」という操作や、折りたたむ操作によって「図形を直線で反転させる」操作に相当するので、幾何の学習に役立つところがたくさんあります。たとえば三角形の辺と辺を合わせるように折ることで、三角形の角の二等分線が１点で交わる内心の定理なども簡単に確認できます。

時間があるようでしたら、折り鶴をつくり、それをまた開いて、そこに表れる折り筋を観察してみましょう。合同な二等辺三角形、相似な三角形のペア、角の二等分や垂直二等分線の存在など、たくさんの図形的な発見があります。

このように試験問題に関係することがわかると「勉強しなきゃ」と思うかもしれませんね。でも、そうすると折り紙を楽しいと思うどころか、逆に嫌気がさしてしまうかもしれません。

それではもったいない！このような試験問題から飛び出して、さらなる折り紙の楽しさ、可能性の広さを見ていきましょう。

折り紙とアート
小さい頃、折り紙は親や先生から教えてもらうものでした。１つ１つの折り操作を正確に同じように再現することで、無事に最後の形に到達します。でも折り紙は与えられた折り方を単純にマネするだけのものではありません。自分で自由に形を作ってもいいのです。平らに折らなくてもいいのですよ（！）。自由に曲がった線で折っても構いません。

下の写真は正方形の紙を曲がった線で自由に折ってみた様子です。このように、ほんの数本の曲線で綺麗な形ができることを知っていましたか？

１枚の紙を折るだけで、誰もが驚くような綺麗で素敵な形が生まれることがあります。そうなると、折り紙も「アート」の仲間入りです。

私は自分の専門であるコンピュータグラフィックスの形状設計の分野の知識を活かし、これまであまり見かけることの無かった、新しい折り紙の形を作ることに挑戦しています。

その１つの分野が、曲線で折る、曲面が含まれる折り紙です。

紙を曲げてできる曲面は、柱面（円柱の仲間）、錐面（円錐の仲間）、接線曲面（空間曲線の接線の集まりでできる面）に限られることが知られていて、それほど自由に形をつくることができません。でも、そこに「折り」を加えることで、さまざまな形を作り出せるようになります。下の写真のような「球体」も作れます。

立体の折り紙は、１枚の紙を曲げてできる曲面を集めて形を作ります。さらに、平面に展開した時に、隙間や歪みができないことが条件になります。このような条件の下で、どのような形ができるだろうか、どのように設計したらよいだろうか、そのような問題を考えることになります。そこには、数学的な考え方が求められることが多いですが、その理論には簡単なものから、難しいものまで幅広くあります。

折り紙は、数学的に考えることと、綺麗な造形を自分の手で作ることの両方を同時に楽しむことができる、すばらしい対象なのです。

こちらのFlickrという写真共有サービスのページ上では、私の作品を多数紹介しています。。
また、「折り紙研究ノート」のページでは、私がまとめた折り紙の研究に関する事柄を掲載しています。これらのページにアクセスし、どうぞ今まで知らなかった折り紙の世界を覗いてみてください。折り紙の形を通して、数学の素晴らしさを感じてもらえればと思います。

※2018年2月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。