私は数理最適化について研究をしています。「数理最適化って何？」と思われる方も多いのではないでしょうか。 これは、実世界の解決すべき様々な問題に対して数理モデルを構築し、計算機を利用して解決策を見出す科学的技法です。この時、数理モデルとして「与えられた制約の下でよりよい目的を達成するための問題」を作ります。もう少し厳密に書くと、ある限られた領域の中で関数 $f(x_1,\ldots,x_n)$ を最大（もしくは最小）にするよう $(x_1,\ldots,x_n)$ を求めなさい、という問題を作り、次のような形（最適化問題と呼ばれます）：

\[ \begin{array}{ll} \mbox{最大化（もしくは最小化）： } & f (x_1,\ldots,x_n) \\ \mbox{条件: } &g_1(x_1,\ldots,x_n) \leq 0 \\ & \hspace{1.5cm}\vdots \\ &g_m(x_1,\ldots,x_n) \leq 0 \\ \end{array} \]

で表します。関数$f$は目的を表現する関数なので、目的関数と呼ばれます。

高校数学IIの教科書を使って勉強したみなさん、何か思い出しませんか？
そうです、 “領域における最大と最小”という項目で、
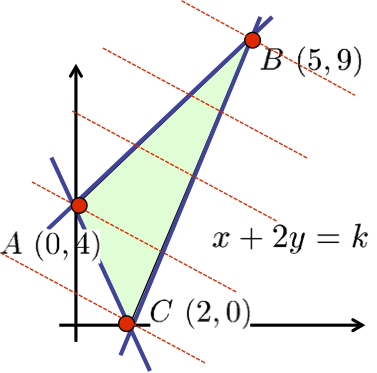
「不等式 $2x+y \geq 4,~ y-x \leq 4, ~3x-y \leq 6$ を 同時に満たす実数 $x,y$ について $x+2y$ の取り得る値の最大値と最小値を求めよ」といった問題を解きましたよね。
まさにこれです。その時には、次のような絵を描いて、直線 $x+2y$ が点 $B$ を通る時に最大値をとり、点 $C$ を通る時に最小値をとることを確認しました。ですが、このやり方だと２〜３次元が限界で、一般の $n$次元の領域の中で最大値、最小値を見つけるのは難しいです。

そこで、絵を描かずに どうやって最大値、最小値つけたらよいか計算手順を考えるのが、私の研究です。

いったいこの問題が解けて何の役に立つのかしら、と疑問を抱いていませんか？
実は、いろいろなところで、私たちは最適化技術の恩恵を受けています。例えば、首都圏でJRや私鉄、地下鉄を乗り継いで目的地まで行こうとすると、いくつものルートが思い浮かんで選択に迷うことがあります。そんな時に携帯やPCから使える乗り換え案内サイトは非常に便利です。いくつもあるルートの中から、最短時間（もしくは最安）のルートを瞬時に導き出してくれるこの便利なツールに最適化技術が使われています。最適なルートを見つける最適化問題の目的関数は“移動時間”や“移動費用”であり、最小値をあたえるようなルートを見つける最適化問題として定式化できます。そして、乗り換え案内サイトでは、瞬時に答えを出すように、解き方に工夫が加えられています。また、コンピュータ囲碁やコンピュータ将棋では最適化技術を使って最善の手が求められています。このように、数理最適化は実社会と密接に結びついた学問です。

みなさんは今まで、いくつも選択肢からどれを選べばいいかわからず悩んだことはありませんか？ お小遣いの制限がある中で、遊園地にも行きたいし、素敵な洋服も欲しい、美味しいものも食べたいし、参考書も買う必要がある。 どれをお小遣いの範囲内で選んだらいいのだろうか．．． そんな時に、目的関数を想定して行動を決めるのはいかがでしょう。若いみなさんにとっての目的は何かしら。今日の楽しさ最大化、かな？それとも将来の夢の実現確率の最大化？ぜひ数理最適化を使ってみてくだい。

※2016年11月掲載。情報は記事執筆時に基づき、現在では異なる場合があります。